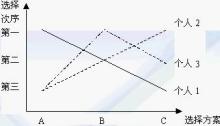
如果一个人具有双峰或多峰偏好，则他从最为偏好的方案偏离时，其偏好程度或效用会下降，但之后会再上升。

布莱克证明了如果假设各个选民的偏好都是单峰偏好，那么最终投票的结果就可以避免阿罗悖论，社会成员个人的偏好之和可以得出确定的唯一的社会总体偏好，而这种社会总体偏好恰好是个人偏好处于所有选民偏好峰的中点上的选民，高于他偏好的选民数量和低于他偏好的选民数量正好相等，这也就是著名的中间投票人模式（median voter models）

。布莱克由于对这个问题的开创性研究而被戈登·塔洛克（Gordon Tullock）称为公共选择学派的奠基人。

邓肯·布莱克认为，通过对个人的偏好进行适当限制，使其适合于某一种类型，则多数决策结果就满足可传递性假定。布莱克对个人偏好提出的特殊类型就是具有单峰形状。这种单峰形状的个人偏好类型可被说明如下 (表1)：

表1　单峰形状的个人偏好

我们可以对A、B、C三种选择目标进行比较：当A与B相比较时，B将胜于A；当B与C比较时，B仍将胜于C；当A与C比较时，C将胜于A。这样，在以上例子中，给定一个特殊的个人偏好结构，多数决策的结果满足可传递性，社会选择的偏好顺序将是BpCpAp(这里p表示“偏好（prefer）”，即前者比后者更可取)。为什么称上表所示的个人偏好类型为单峰型呢？可以用下图加以说明。

（图1）

假定有三个人l、2、3，每人共同面临A、B、C三种选择，A代表政府高水平的预算，B代表中等水平的预算，C代表低水平的预算。每个人的偏好顺序以他对于这三个选择方案的排列顺序表示出来。表4-1代表这三个人的偏好顺序:

表2　个人的偏好顺序

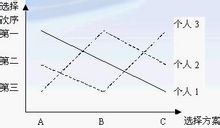
（图2）

图2表示表2上的个人偏好结构，而图1表示表1上的个人偏好结构。图2与图1的区别在于，在图4-2中，三个人的偏好线都是单峰形状的。单峰偏好意味着人们最理想的结果只有一个，对于这个惟一的最理想目标的偏离，无论是正的方向，还是负的方向，都是坏事情，都将使他们的福利水平降低。例如，对于个人1来讲，如果选择方案依照A、B、C的顺序排列，他会认为境况逐渐变坏；对于个人2来讲，如果选择方案依照A、B、C的顺序排列，他会认为境况逐渐变好；对于个人3来讲，只要偏离了B方案，不论是向哪个方向偏离，他都认为境况变坏。而在图4-1中，个人3的偏好线是双峰形的（多峰偏好），该线先是从某一峰顶上往下降，然后又往另一峰顶上升。多峰偏好则意味着人们最理想的结果不止一个。最初，当人们偏离其最偏好的选择目标时，境况会因此变坏，若继续沿着这个方向运动，其境况则会最终变好。

对比多峰偏好，对于单峰型的个人偏好结构可以有以下结论：

1、在单峰型的个人偏好结构中，多数决策的结果具有稳定性。在2的表式中，社会偏好不具有传递性，是循环的，于是，投票结果是不确定的。现在，在单峰偏好下，循环被打破了，从而产生了一个稳定的结果。

2、单峰偏好虽然克服了投票悖论，但它违反了阿罗关于“无限制的定义域”的假定，即单峰偏好是依靠把个人偏好限制在单峰状态为前提的。

3、单峰状态究竟在实际中是否存在？布莱克认为，在大多数场合，个人的偏好结构会呈现出单峰形。为什么呢？由于A代表低水平的预算，B代表中等水平的预算，C代表高水平的预算，在概率上说，CpApBp的个人偏好顺序出现的可能性很小，因为绝大多数人不会既认为高额预算比低额预算好，又认为低额预算比中等规模的预算好。

1970年，图洛克与坎贝尔(Campbell)在《小型投票体系的计算机模拟》(Computer simulation of a small voting system)一文中指出，在现实世界中，投票者的人数总是大大超过供投票选择的社会状态的个数的。这时，出现投票悖论的概率是如此的小，以至于在实际中可以不考虑它。这时，出现一致的概率就很高，而再提出或拥护另一个选择方案的成本会高于该方案能带来的利益。如果实际的多数投票结果确实靠近中间状态，则该结果将被大家所接受。虽然，图洛克的分析是否有效，这个问题是有待于经验证明的，但是，可以肯定的是，图洛克这一段话是非常有助于说明直接民主投票制与间接投票制之间的差异的。

1、在直接民主投票制下，参加投票的人数总是大大超过被投票表决的方案个数的，这时出现投票悖论概率很小。

2、在代表制投票方式(间接投票制)下，如在英国，投票者总是限于保守党、工党与别的大党之间，由于投票者数目减少了，就使投票难以达到一致的结果。

这说明，在一个社会可供选择的状态的个数已定的前提下，决策程序越是不民主，则投票结果就越是不确定、不稳定，政府政策就越是易变，于是，也会越是依赖于专制型决策。